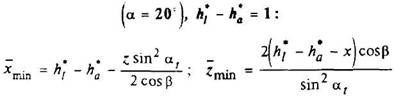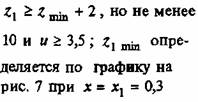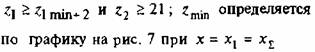Термины и обозначения приведены в табл. 1, определения терминов см. ГОСТ 16530—83 и 16531-83.
[gview file=»https://www.cb-online.ru/wp-content/uploads/2014/05/GOST-16530—83.pdf»]
[gview file=»https://www.cb-online.ru/wp-content/uploads/2014/05/GOST-16531—83.pdf»]
1. Термины и обозначения цилиндрических зубчатых передач
Делительное межосевое расстояние — a
Межосевое расстояние — aw
Ширина венца цилиндрического зубчатого колеса — b
Рабочая ширина венца зубчатой передачи — bw
Радиальный зазор пары исходных контуров — c
Коэффициент радиального зазора нормального исходного контура – c*
Высота зуба цилиндрического зубчатого колеса — h
Высота делительной головки зуба цилиндрического зубчатого колеса — ha
Коэффициент высоты головки исходного контура – ha*
Высота до хорды зуба колеса — 
Высота до постоянной хорды зуба — 
Высота до хорды дуги окружности — 
Глубина захода зубьев колеса, а также глубина захода зубьев исходных реек — 
Высота делительной ножки зуба колеса — hf
Граничная высота зуба колеса — hl
Делительный диаметр зубчатого колеса — d
Диаметр вершин зубьев колеса — da
Основной диаметр зубчатого колеса — db
Диаметр впадин зубчатого колеса — df
Диаметр окружности граничных точек зубчатого колеса — dl
Начальный диаметр зубчатого колеса — dw
Радиус зубчатого колеса — r
Расчетный модуль цилиндрического зубчатого колеса — m
Нормальный модуль зубьев — mn
Окружной модуль зубьев (торцовый) — mt
Шаг эвольвентного зацепления — pb
Нормальный шаг зубьев рейки — pn
Торцовый шаг зубьев рейки — pt
Осевой шаг зубьев рейки — px
Основной нормальный шаг зубьев — pbn
Основной окружной шаг зубьев — pbt
Основная нормальная толщина зуба — sbn
Постоянная хорда зуба — 
Нормальная толщина зуба рейки — sn
Осевая толщина зуба рейки — sx
Торцовая толщина зуба рейки — st
Толщина по хорде зуба — 
Окружная толщина на заданном диаметре dy — sty
Толщина по хорде — 
Длина обшей нормали зубчатого колеса — W
Коэффициент смещения исходного контура — x
Коэффициент наименьшего смещения исходного контура — xmin
Коэффициент суммы смещений хΣ
Коэффициент воспринимаемого смещения — у
Коэффициент уравнительного смещения — Δу
Число зубьев зубчатого колеса (число зубьев секторно-зубчатого колеса) — z
Наименьшее число зубьев, свободное от подрезания — zmin
Число зубьев в длине обшей нормали — zw
Нормальный боковой зазор эвольвентной цилиндрической зубчатой передачи — jn
Эвольвентный угол профиля зуба – inv a
Эвольвентный угол, соответствующий точке профиля на окружности dy– inv ay
Частота вращения зубчатого колеса в минуту — n
Передаточное число зубчатой передачи (z2/z1; d2/d1; n1/n2) — u
Угол профиля зуба исходного контура в нормальном сечении — a
Угол профиля зуба в торцовом сечении — at
Угол зацепления — atw
Угол профиля в точке на концентрической окружности заданного диаметра dy — ay
Угол наклона линии зуба соосной цилиндрической поверхности диаметраdy— βy
Угол наклона линии зуба — β
Основной угол наклона линии зуба (косозубого колеса на его основном цилиндре) — βb
Угол развернутости эвольвенты зуба — v
Половина угловой толщины зуба — ψ
Половина угловой толщины зуба эквивалентного зубчатого колеса, соответствующая концентрической окружности диаметра dy/cos2βy — ψyv
Угловая скорость — ω
Шестерня — зубчатое колесо передачи с меньшим числом зубьев, колесо — с большим числом зубьев. При одинаковом числе зубьев зубчатых колес передачи шестерней называют ведущее зубчатое колесо, а колесом — ведомое. Индекс 1 — для величин, относящихся к шестерне, индекс 2 — относящихся к колесу.
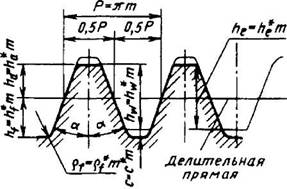
Рис. 1. Исходный контур зубчатых цилиндрических колес эвольвентного зацепления по ГОСТ 13755—81 и конических колес с прямыми зубьями по ГОСТ 13754— 81
Индекс n — для величин, относящихся к нормальному сечению, t — к окружному (торцовому) сечению. В тех случаях, когда не может быть разночтения и неясности, индексы n и t можно исключить.
Термины параметров нормального исходного контура и нормального исходного производящего контура, выраженных в долях модуля нормального исходного контура, образуют добавлением слова «коэффициент» перед термином соответствующего параметра.
Обозначения коэффициентов соответствуют обозначениям параметров с добавлением знака «*», например коэффициент радиального зазора пары исходных контуров с*.
Модули (по ГОСТ9563—60). Стандарт распространяется на эвольвентные цилиндрические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанавливает:
для цилиндрических колес — значения нормальных модулей;
для конических колес — значения внешних окружных делительных модулей.
Числовые значения модулей:
|
Ряд 1 |
Ряд 2 |
Ряд 1 |
Ряд 2 |
Ряд 1 |
Ряд 2 |
Ряд 1 |
Ряд 2 |
|
1 |
1,125 |
— |
— |
5 |
5,5 |
12 |
14 |
|
1,25 |
1,375 |
2,5 |
2,75 |
6 |
7 |
16 |
18 |
|
1.5 |
1..75 |
3 |
3,5 |
8 |
9 |
20 |
22 |
|
2 |
2,25 |
4 |
4,5 |
10 |
11 |
25 |
28 |
|
32 |
36 |
||||||
Примечания:
1. При выборе модулей ряд 1 следует предпочитать ряду 2.
2. Для цилиндрических зубчатых колес допускается:
а) в тракторной промышленности применение модулей 3,75; 4,25 и 6,5мм;
б) в автомобильной промышленности применение модулей, отличающихся от установленных в настоящем стандарте;
в) в редукторостроении применение модулей 1,6; 3,15; 6,3; 12,5м.
3. Для конических зубчатых колес допускается:
а) определять модуль на среднем конусном расстоянии;
б) в технически обоснованных случаях применение модулей, отличающихся от указанных в таблице.
4. Стандарт предусматривает применение модулей в диапазоне значений от 0,05 до 100мм.
Исходный контур цилиндрических зубчатых колес. Под исходным контуром колес (рис. 1) подразумевают контур зубьев рейки в нормальном к направлению зубьев сечении. Радиальный зазор с = 0,25m, радиус кривизны переходной кривой зуба pf = 0.4m. Допускается увеличение радиуса рfесли это не нарушает правильности зацепления, и увеличение с до 0,35m при обработке колес долбяками и шеверами и до 0,4m при шлифовании зубьев.
Для цилиндрических колес внешнего зацепления при окружной скорости более указанной в табл. 2 применяют исходный контур с модификацией профиля головки зуба (рис. 2). При этом линия модификации — прямая, коэффициент модификации hg* должен быть не более 0,45, а коэффициент глубины модификации Δ* — не более 0,02.
Рекомендуемые значения коэффициента Δ* приведены в табл. 3.
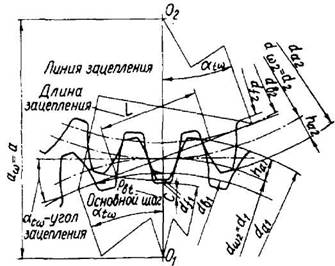
Основные элементы зубчатого зацепления указаны на рис. 3 и 4 в соответствии с обозначением по табл. 1.
Смещение колес зубчатых передач с внешним зацеплением. Чтобы повысить прочность зубьев на изгиб, снизить контактные напряжения на их поверхности и уменьшить износ за счет относительного скольжения профилей, рекомендуется производить смешение инструмента для цилиндрических (и конических) зубчатых передач, у которых z1 ≠ z2. Наибольший результат достигается в следующих случаях:
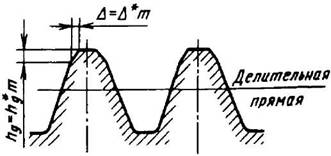
Рис. 2. Исходный контур с профильной модификацией
2. Окружная скорость колес в зависимости от их точности
|
Тип колес |
Окружная скорость в м/спри степени точности колеса по ГОСТ 1643-81 |
||
|
6 |
7 |
8 |
|
|
Прямозубые |
10 |
6 |
4 |
|
Косозубые |
16 |
10 |
6 |
3. Коэффициент глубины модификации Δ* в зависимости от модуля и степени точности
|
Модуль m,мм |
Степень точности по нормам плавности работы по ГОСТ 1643-81 |
||
|
6 |
7 |
8 |
|
|
До 2 |
0,010 |
0,015 |
0,020 |
|
Св. 2 до 3,5 |
0,009 |
0,012 |
0,018 |
|
» 3,5 » 6,3 |
0,008 |
0,010 |
0,035 |
|
» 6,3 » 10 |
0,006 |
0,008 |
0,012 |
|
» 10 » 16 |
0,005 |
0,007 |
0,010 |
|
» 16 » 25 |
— |
0,006 |
0,009 |
|
» 25 » 40 |
— |
— |
0,008 |
1) при смещении передач, у которых шестерня имеет малое число зубьев (z1 < 17), так как при этом устраняется подрез у корня зуба;
2) при больших передаточных числах, так как в этом случае значительно снижается относительное скольжение профилей.
Рис. 3
Рис. 4
Положение исходного производящего контура относительно нарезаемого колеса, при котором делительная прямая рейка касается делительной окружности колеса, называют номинальным положением (рис. 5, а). Колесо, зубья которого образованы при номинальном положении исходной производящей рейки, называют колесом, нарезанным без смешения исходного контура (по старой терминологии — некорригированное колесо).
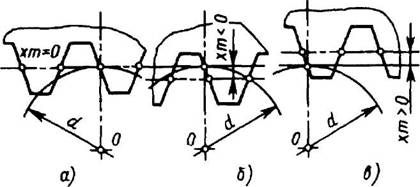
Рис. 5. Положение производящего реечного контура относительно заготовки:
а — номинальное; б — с отрицательным смещением; в — с положительным смещением
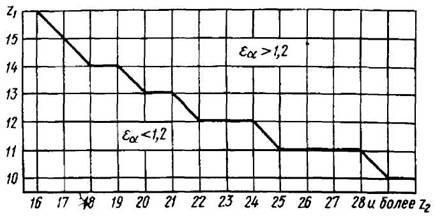
Рис. 6. График для определения нижнего предельного значения z1 в зависимости от z2 при которых
εа = 1,2 (x1= х2 = 0,5)
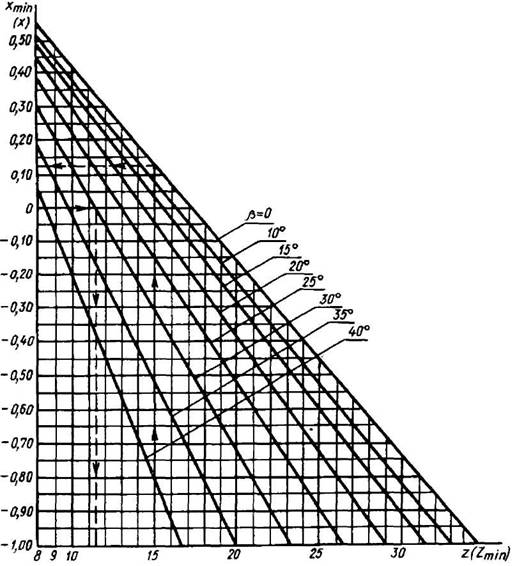
Рис. 7. График для определения хmin в зависимости от z и β или zmin — х и β
(округляется до ближайшего большего целого числа)
Примеры.
1. Дано: z = 15; β = 0. По графику определяем хmin = 0,12 (см. штриховую линию).
2. Дано: х = 0; β = 30°. По графику определяем наименьшее число зубьев  = 12 (cм. штриховую линию)
= 12 (cм. штриховую линию)
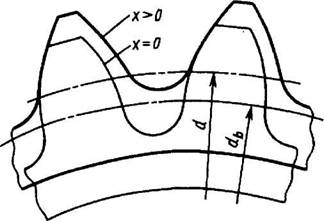
Рис. 8. Влияние смещения исходного контура на геометрию зубьев
Если исходная производящая рейка в станочном зацеплении смещена из номинального положения и установлена так, что ее делительная прямая не касается делительной окружности нарезаемого колеса, то в результате обработки получится колесо, нарезанное со смещением исходного контура (по старой терминологии — корригированное колесо).
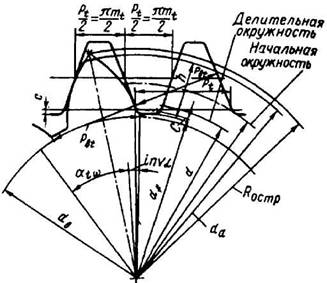
Рис. 9. Зацепление (в сечении, параллельном торцовому) зубчатого колеса со смещением с исходной производящей рейкой
4. Коэффициенты смещения у зубчатых колес прямозубой передачи
|
Коэффициент смещения |
Область применения |
|||
|
у шестерни х1 |
у колеса х2 |
|||
|
0 |
0 |
Межосевое расстояние aw задано равным 0,5(z1 + z2)m или не задано |
Кинематические передачи |
z1 ≥ 17 |
|
0,3 |
-0,3 |
12 ≤ z1 < 16 и z2 ≥ 22 |
||
|
0 |
0 |
Межосевое расстояние aw задано равным 0,5(z1 + z2)m |
Силовыепередачи |
z1 ≥ 21 |
|
0,3 |
-0,3 |
14 ≤ z1 ≤ 20 и u ≥ 3,5 |
||
|
0 |
0 |
Межосевое расстояние aw не задано |
z1> 30 |
|
|
0,5 |
0,5 |
10 ≤ z1 ≤ 30. В пределах 10 ≤ z1 ≤ 16 нижнее предельное значение z1 определяется по графику (рис.6) |
||
5. Коэффициент смещения у зубчатых колес косозубой и шевронной передач
|
Коэффициент смещения |
Область применения |
|||
|
у шестерни х1 |
у колеса х2 |
|||
|
0 |
0 |
Межосевое расстояние aw задано равным (z1+z2)m/(2cosβ) или не задано |
Кинематическиепередачи |
|
|
0,3 |
-0,3 |
|||
|
0 |
0 |
Силовыепередачи |
||
|
0,3 |
-0,3 |
|||
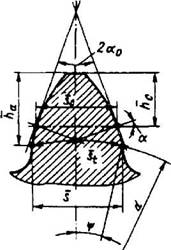
Рис. 10. Толщина зуба по постоянной хорде и высота до постоянной хорды в нормальном сечении
Расстояние от делительной прямой исходной производящей рейки (или исходного контура) до делительной окружности колеса является величиной смещения.
Отношение смещения исходного контура к расчетному модулю называют коэффициентом смещения (х).
Если делительная прямая исходного контура пересекает делительную окружность зубчатого колеса (рис. 5, б), смещение называют отрицательным (х < 0), если не пересекает и не соприкасается (рис. 5, в) — положительным (х > 0). При номинальном положении исходного контура смещение равно нулю (х = 0).
Коэффициент смещения х обеспечивается установкой инструмента относительно заготовки зубчатого колеса в станочном зацеплении.
Коэффициенты смещения у зубчатых колес рекомендуется выбирать по табл. 4 для прямозубой передачи и по табл. 5 — для косозубой и шевронной передач.
Основные элементы зубчатого зацепления со смещением указаны на рис. 8, 9, 10.
6. Разбивка коэффициента суммы смещения xΣ у прямозубой передачи на составляющие х1 и х2
|
Коэффициент суммы смещения хΣ |
Коэффициент смещения |
Область применения |
||
|
у шестерни х1 |
у колеса x2 |
|||
|
0 < xΣ ≤ 0,5 |
xΣ |
0 |
Кинематические передачи |
|
|
Силовые передачи |
||||
|
0,5 < хΣ ≤ 1 |
0,5 |
хΣ — 0,5 |
Кинематические передачи |
|
|
Силовые передачи |
||||
Примечания:
1. При заданном межосевом расстоянии aw требуемое значение коэффициента суммы смещений хΣ можно получить за счет изменения числа зубьев z1 или z2, если это изменение допускается.
2. При 0.3 < хΣ < 0,7 и u < 2 наибольшая скорость скольжения в зацеплении будет большей, чем в передаче без смещения.
3. При u = 1 рекомендуется x1 = x2 = 0,5хΣ.
7. Разбивка коэффициента суммы смещения xΣ у косозубой или шевронной передачи на составляющие х1 и x2
|
Коэффициент суммы смещения хΣ |
Коэффициент смещения |
Область применения |
||
|
у шестерни х1 |
у колеса x2 |
|||
|
0 < xΣ ≤ 0,5 |
xΣ |
0 |
Кинематическиепередачи |
|
|
0 < xΣ ≤ 0,5 |
xΣ |
0 |
Силовыепередачи |
|
Примечания:
1. При заданном межосевом расстоянии aw требуемое значение коэффициента суммы смещений хΣ можно получить за счет изменения числа зубьев z1 или z2, угла наклона β, если эти изменения допускаются.
2. При хΣ > 0,3 и u < 2 наибольшая скорость скольжения в зацеплении будет большей, чем в передаче без смещения.
3. При u = 1 рекомендуется х1 = х2 = 0,5xΣ.
8. Значения наименьшего числа зубьев zmin зубчатого колеса с коэффициентом смещения х = 0 при станочном зацеплении с исходной производящей рейкой
|
βº |
zmin |
βº |
zmin |
βº |
zmin |
|
До 12 |
17 |
Св. 21до 24 |
14 |
Св. 31 до 34 |
11 |
|
Св. 12 » 17 |
16 |
» 24 » 28 |
13 |
» 34 |
10 |
|
» 17 » 21 |
15 |
» 28 » 31 |
12 |
||
[Цилиндрические зубчатые передачи] Далее »